Climate Sensitivity Reconsidered Part 3

A special report from Christopher Monckton of Brenchley to all Climate Alarmists, Consensus Theorists and Anthropogenic Global Warming Supporters

Continues from Part 2

Figure 6
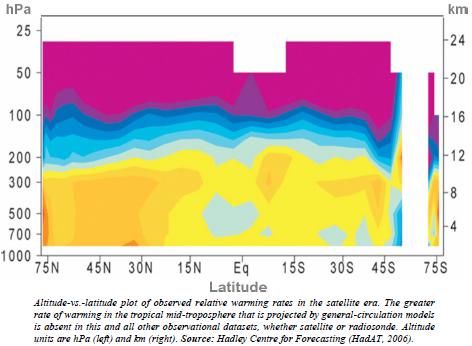
The absent fingerprint of anthropogenic greenhouse warming

None of the temperature datasets for the tropical surface and mid-troposphere shows the strong differential warming rate predicted by the IPCC’s models. Thorne et al. (2007) suggested that the absence of the mid-tropospheric warming might be attributable to uncertainties in the observed record: however, Douglass et al. (2007) responded with a detailed statistical analysis demonstrating that the absence of the projected degree of warming is significant in all observational datasets.  Allen et al. (2008) used upper-atmosphere wind speeds as a proxy for temperature and concluded that
the projected greater rate of warming at altitude in the tropics is occurring in reality. However, satellite records, such as the RSS temperature trends at varying altitudes, agree with the radiosondes that the warming differential is not occurring: they show that not only absolute temperatures but also warming rates decline with altitude.  There are two principal reasons why the models appear to be misrepresenting the tropical atmosphere so starkly. First, the concentration of water vapor in the tropical lower troposphere is already so great that there is little scope for additional greenhouse-gas forcing. Secondly, though the models assume that the concentration of water vapor will increase in the tropical mid-troposphere as the space occupied by the atmosphere warms, advection transports much of the additional water vapor poleward
from the tropics at that altitude.

Since the great majority of the incoming solar radiation incident upon the Earth strikes the tropics, any reduction in tropical radiative forcing has a disproportionate effect on mean global forcings. On the basis of Lindzen (2007), the anthropogenic-ear radiative forcing as established in Eqn. (3) are divided by 3 to take account of the observed failure of the tropical mid-troposphere to warm as projected by the models –

ΔF2x ≈ 3.405 / 3 ≈ 1.135 Wm–2. (17)

The “no-feedbacks” climate sensitivity parameter κ reconsidered The base climate sensitivity parameter κ is the most influential of the three factors of ΔTλ: for the final or “with-feedbacks” climate sensitivity parameter λ is the product of κ and the feedback factor f, which is itself dependent not only on the sum b of all climate-relevant temperature feedbacks but also on κ.  Yet κ has received limited attention in the literature. In IPCC (2001, 2007) it is not mentioned.
However, its value may be deduced from hints in the IPCC’s reports. IPCC (2001, ch. 6.1) says:

“The climate sensitivity parameter (global mean surface temperature response ΔTS to the radiative forcing
ΔF) is defined as ΔTS / ΔF = λ {6.1} (Dickinson, 1982; WMO, 1986; Cess et al., 1993). Equation {6.1} is defined for the transition of the surface-troposphere system from one equilibrium state to another in response to an externally imposed radiative perturbation. In the one-dimensional radiative-convective models, wherein the concept was first initiated, λ is a nearly invariant parameter (typically, about 0.5 °K W−1 m2; Ramanathan et al., 1985) for a variety of radiative forcings, thus introducing the notion of a possible universality of the relationship between forcing and response.”

Since λ = κf = κ(1 – bκ)–1 (Eqns. 1, 2), where λ = 0.5 °K W–1 m2 and b ≈ 2.16 W m–2 °K–1 (Eqn. 12), it is simple to calculate that, in 2001, one of the IPCC’s values for f was 2.08. Thus the value f = 3.077 in IPCC (2007) represents a near-50% increase in the value of f in only five years. Where f = 2.08, κ = λ / f ≈ 0.5 / 2.08 ≈ 0.24 °K W–1 m2, again substantially lower than the value implicit in IPCC (2007).

Some theory will, therefore, be needed.

The fundamental equation of radiative transfer at the emitting surface of an astronomical body, relating changes in radiant-energy flux to changes in temperature, is the Stefan-Boltzmann equation – F = ε σ T4 W m–2, (18)
where F is radiant-energy flux at the emitting surface; ε is emissivity, set at 1 for a blackbody that absorbs and emits all irradiance reaching its emitting surface (by Kirchhoff’s law of radiative transfer, absorption and emission are equal and simultaneous), 0 for a white body that reflects all irradiance, and (0, 1) for a graybody that partly absorbs/emits and partly reflects; and σ ≈ 5.67 x 10–8 is the Stefan-Boltzmann constant.  Differentiating Eqn. (18) gives –

κ = dT / dF = (dF / dT)–1 = (4 ε σ T3)–1 °K W–1 m2. (19) Outgoing radiation from the Earth’s surface is chiefly in the near-infrared. Its peak wavelength λmax is determined solely by the temperature of the emitting surface in accordance with Wien’s Displacement Law, shown in its simplest form in Eqn. (20):

λmax = 2897 / TS = 2897 / 288 ≈ 10 μm. (20)

Since the Earth/troposphere system is a blackbody with respect to the infrared radiation that Eqn. (20) shows we are chiefly concerned with, we will not introduce any significant error if ε = 1, giving the blackbody form of Eqn. (19) –

κ = dT / dF = (4 σ T3)–1 °K W–1 m2. (21)

At the Earth’s surface, TS ≈ 288 °K, so that κS ≈ 0.185 °K W–1 m2. At the characteristic-emission level, ZC, the variable altitude at which incoming and outgoing radiative fluxes balance, TC ≈ 254 °K, so that κC ≈ 0.269 °K W–1 m2. The value κC ≈ 0.24, derived from the typical final-sensitivity value λ = 0.5 given in IPCC (2001), falls between the surface and characteristic-emission values for κ.

However, the IPCC, in its evaluation of κ, does not follow the rule that in the Stefan-Boltzmann equation the temperature and radiant-energy flux must be taken at the same level of the atmosphere.  The IPCC’s value for κ is dependent upon temperature at the surface and radiant-energy flux at the tropopause, so that its implicit value κ ≈ 0.313 °K W–1 m2 is considerably higher than either κS or κC.  IPCC (2007) cites Hansen et al. (1984), who say –

“Our three-dimensional global climate model yields a warming of ~4 ºC for … doubled CO2. This indicates a net feedback factor f = 3-4, because [the forcing at CO2 doubling] would cause the earth’s surface temperature to warm 1.2-1.3 ºC to restore radiative balance with space, if other factors remained unchanged.”

Hansen says dF2x is equivalent to a 2% increase in incoming total solar irradiance (TSI). Top-ofatmosphere
TSI S ≈ 1368 W m2, albedo α = 0.31, and Earth’s radius is r. Then, at the characteristic
emission level ZC,

FC = S(1 – α)(πr2 / 4πr2) ≈ 1368 x 0.69 x (1/4) ≈ 236 Wm–2. (22)

Thus a 2% increase in FC is equivalent to 4.72 W m–2, rounded up by Hansen to 4.8 W m–2, implying that κ ≈ 1.25 / 4.8 ≈ 0.260 °K W–1 m2. However, Hansen, in his Eqn. {14}, prefers 0.29 Wm–2.  Bony et al. (2006), also cited by IPCC (2007), do not state a value for κ. However, they say – “The Planck feedback parameter [equivalent to κ –1] is negative (an increase in temperature enhances the long-wave emission to space and thus reduces R [the Earth’s radiation budget]), and its typical value for the earth’s atmosphere, estimated from GCM calculations (Colman 2003; Soden and Held 2006), is ~3.2 W m2 ºK–1 (a value of ~3.8 W m2 ºK–1 is obtained by defining [κ –1] simply as 4σT3, by equating the global
mean outgoing long-wave radiation to σT4 and by assuming an emission temperature of 255 ºK).” Bony takes TC ≈ 255 °K and FC ≈ 235 W m–2 at ZC as the theoretical basis for the stated prima facie value κ –1 ≈ TC / 4FC ≈ 3.8 W m2 ºK–1, so that κ ≈ 0.263 ºK W–1 m2, in very close agreement with Hansen. However, Bony cites two further papers, Colman (2003) and Soden & Held (2006), as justification for the value κ –1 ≈ 3.2 W m2 ºK–1, so that κ ≈ 0.313 ºK W–1 m2.  Colman (2003) does not state a value for κ, but cites Hansen et al. (1984), rounding up the value κ ≈ 0.260 °K W–1 m2 to 0.3 °K W–1 m2 – “The method used assumes a surface temperature increase of 1.2 °K with only the CO2 forcing and the
‘surface temperature’ feedback operating (value originally taken from Hansen et al. 1984).”

Soden & Held (2006) likewise do not declare a value for κ. However, we may deduce their implicit central estimate κ ≈ 1 / 4 ≈ 0.250 °K W–1 m2 from the following passage – “The increase in opacity due to a doubling of CO2 causes [the characteristic emission level ZC] to rise by ~150 meters. This results in a reduction in the effective temperature of the emission across the tropopause by ~(6.5K/km)(150 m) ≈ 1 K, which converts to 4 W m–2 using the Stefan-Boltzmann law.”  Thus the IPCC cites only two papers that cite two others in turn. None of these papers provides any theoretical or empirical justification for a value as high as the κ ≈ 0.313 °K W–1 m2 chosen by the IPCC.

Kiehl (1992) gives the following method, where FC is total flux at ZC:

κS = TS / (4FC) ≈ 288 / (4 x 236) ≈ 0.305 °K W–1 m2. (23)

Hartmann (1994) echoes Kiehl’s method, generalizing it to any level J of an n-level troposphere thus:

κJ = TJ / (4FC)
= TJ / [S(1 – α)]
≈ TJ / [1368(1 – 0.31)] ≈ TJ / 944 °K W–1 m2. (24)

Table 2 summarizes the values of κ evident in the cited literature, with their derivations, minores priores. The greatest value, chosen in IPCC (2007), is 30% above the least, chosen in IPCC (2001).  However, because the feedback factor f depends not only upon the feedback-sum b ≈ 2.16 W m–2 °K–1  but also upon κ, the 30% increase in κ nearly doubles final climate sensitivity:

Table 2
Values of the “no-feedbacks” climate sensitivity parameter κ

The value of κ cannot be deduced by observation, because temperature feedbacks are present and cannot be separately measured. However, it is possible to calculate κ using Eqn. (6), provided that the temperature change ΔTλ, radiative forcings ΔF2x, and feedback-sum b over a given period are known.  The years 1980 and 2005 will be compared, giving a spread of a quarter of a century. We take the feedback-sum b = 2.16 W m–2 °K–1 and begin by establishing values for ΔF and ΔT:  CO2 concentration: 338.67 ppmv 378.77 ppmv ΔF = 5.35 ln (378.77/338.67) = 0.560 W m–2 Anomaly in TS: 0.144 °K 0.557 °K ΔT = 0.412 °K (NCDC) Anomaly halved: ΔT = 0.206 °K (McKitrick) (25) CO2 concentrations are the annual means from 100 stations (Keeling & Whorf, 2004, updated). TS values are NCDC annual anomalies, as five-year means centered on 1980 and 2005 respectively. Now, depending on whether the NCDC or implicit McKitrick value is correct, κ may be directly evaluated:

NCDC: κ = ΔT / (ΔF + bΔT) = 0.412 / (0.560 + 2.16 x 0.412) = 0.284 °KW–1 m2
McKitrick: κ = ΔT / (ΔF + bΔT) = 0.206 / (0.599 + 2.16 x 0.206) = 0.197 °KW–1 m2
Mean: κ = (0.284 + 0.197) / 2 = 0.241 °KW–1 m2 (26)

We assume that Chylek (2008) is right to find transient and equilibrium climate sensitivity near identical; that all of the warming from 1980-2005 was anthropogenic; that the IPCC’s values for forcings and feedbacks are correct; and, in line 2, that McKitrick is right that the insufficiently corrected heat-island effect of rapid urbanization since 1980 has artificially doubled the true rate of temperature increase in the major global datasets.

With these assumptions, κ is shown to be less, and perhaps considerably less, than the value implicit in IPCC (2007). The method of finding κ shown in Eqn. (24), which yields a value very close to that of IPCC (2007), is such that progressively smaller forcing increments would deliver progressively larger temperature increases at all levels of the atmosphere, contrary to the laws of thermodynamics and to the Stefan-Boltzmann radiative-transfer equation (Eqn. 18), which mandate the opposite. It is accordingly necessary to select a value for κ that falls well below the IPCC’s value. Dr. David Evans (personal communication, 2007) has calculated that the characteristic-emission-level value of κ should be diminished by ~10% to allow for the non-uniform latitudinal distribution of incoming solar radiation, giving a value near-identical to that in Eqn. (26), and to that implicit in IPCC (2001), thus –

κ = 0.9TC / [S(1 – α)]
≈ 0.9 x 254 / [1368(1 – 0.31)] ≈ 0.242 °K W–1 m2 (27)

The feedback factor f reconsidered

The feedback factor f accounts for two-thirds of all radiative forcing in IPCC (2007); yet it is not expressly quantified, and no “Level Of Scientific Understanding” is assigned either to f or to the two variables b and κ upon which it is dependent.
Several further difficulties are apparent. Not the least is that, if the upper estimates of each of the climate-relevant feedbacks listed in IPCC (2007) are summed, an instability arises. The maxima are –

Water vapor feedback 1.98 W m–2 K–1
Lapse rate feedback –0.58 W m–2 K–1
Surface albedo feedback 0.34 W m–2 K–1
Cloud albedo feedback 1.07 W m–2 K–1
CO2 feedback 0.57 W m–2 K–1
Total feedbacks b 3.38 Wm–2 K–1 (28)

Continue to Part 4